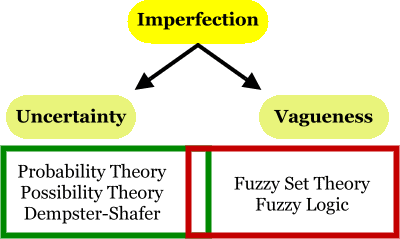
Fig.1. Imperfection and theories to handle it.
Fuzzy logic and probability theory are the most powerful tools to overcome the imperfection (see Fig.1). Fuzzy logic is mainly responsible for representation and processing of vague data (ill-defined, fuzzy). Probability theory is mainly responsible for representation and processing of uncertainty (randomness).

Following table clarifies the differences between the two theories.
|
Probability Measure |
Membership Function |
|
Calculates the probability that an |
Calculates the membership of a |
|
Before an event happens |
After it happened |
|
Measure Theory |
Set Theory |
|
Domain is 2U (Boolean Algebra) |
Domain is [0,1]U (Cannot be a Boolean Algebra) |
Consider the following statements:
In such cases (which are very usual in pattern recognition, for instance), we are interested in probability of an event that cannot be defined exactly. Therefore, the only sophisticated way is to calculate the probability of a fuzzy event represented by a fuzzy set:
|
Probability space |
||
|
Membership function |
||
|
The probability of the fuzzy event F |
||
For more details see following papers/books:
Probability measures of fuzzy events, L.A.Zadeh, Journal Math. Anal. Appl., vol 23, pp. 421-427, 1968
Fuzzy Sets as a basis for a theory of possibility, L.A. Zadeh, Fuzzy Sets and Systems, vol. 1, pp. 3-28, 1978
Possibility Theory, D.Dubois, H. Prade, Plenum Press, 1988
Fuzzy sets and probability : Misunderstandings, bridges and gaps, D.Dubois, H. Prade, Proc. of the Second IEEE Inter. Conf. on Fuzzy Systems, volume 2, pp. 1059-1068, 1993